Topology Optimization (Part 1)

 

Topology optimization overview

In Part 1 and Part 2 of this article I will dive a little deeper into the background of Topology Optimization and attempt to give some insights into what controls we can exert on the process to improve the relevance to our design goals.

Figure 1 shows a typical topology optimization analysis, based on the geometry, materials and loading definition given in the GE/GRABCAD challenge, references 1 and 2, I hasten to add that my version is not a contender!

I do recommend trying the GE/GRABCAD challenge as your own benchmarking exercise. The specification, initial geometry and full set of 638(!) results are available at reference 1. Various assessment papers have also been written which critique the winning designs from structural and manufacturing perspectives.

 

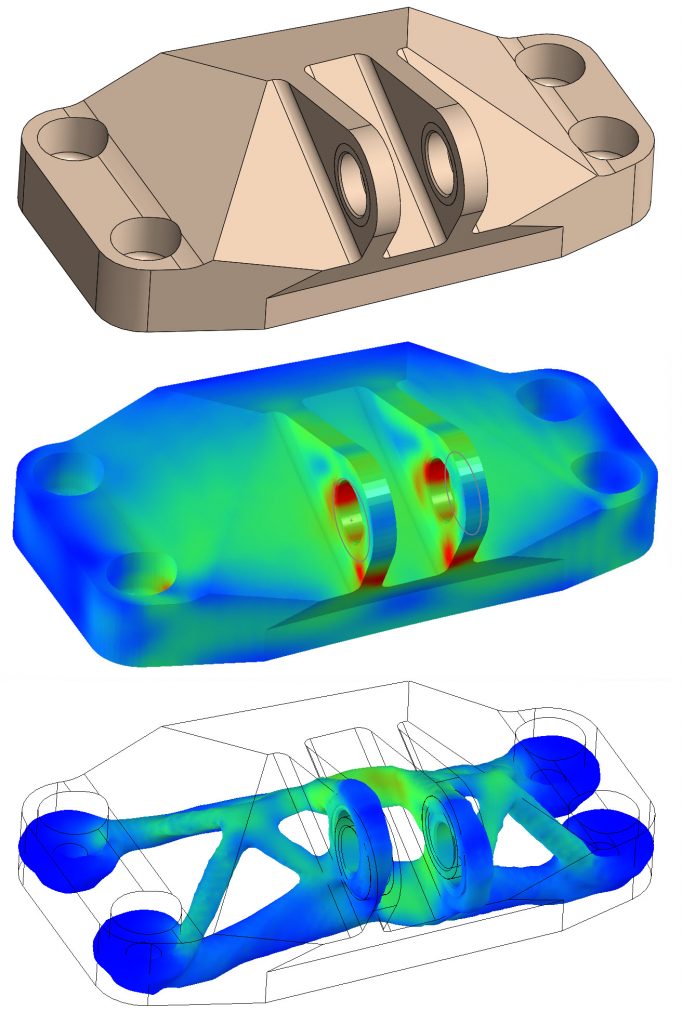 Figure 1 (a) top, initial design space. 1(b) middle, initial analysis. 1(c) bottom, final analysis.

 

The basic idea behind topology optimization is to define a design space and then mesh that with a very regular array of elements. In some cases, this will be an arbitrary 3D or 2D space, in other cases, as shown in Figure 1(a), the mesh will follow an initial scheme. We will look at the implications of this distinction in Part 2.  The boundary conditions and loading are defined as normal in an FEA solution and analysis starts with the full design space as shown in Figure 1(b). Material is progressively removed using a target volume reduction, until a final iteration, as shown in Figure 1(c). The final design is assumed to be optimized to a defined level of efficiency at that target volume.

Topology optimization methods

 

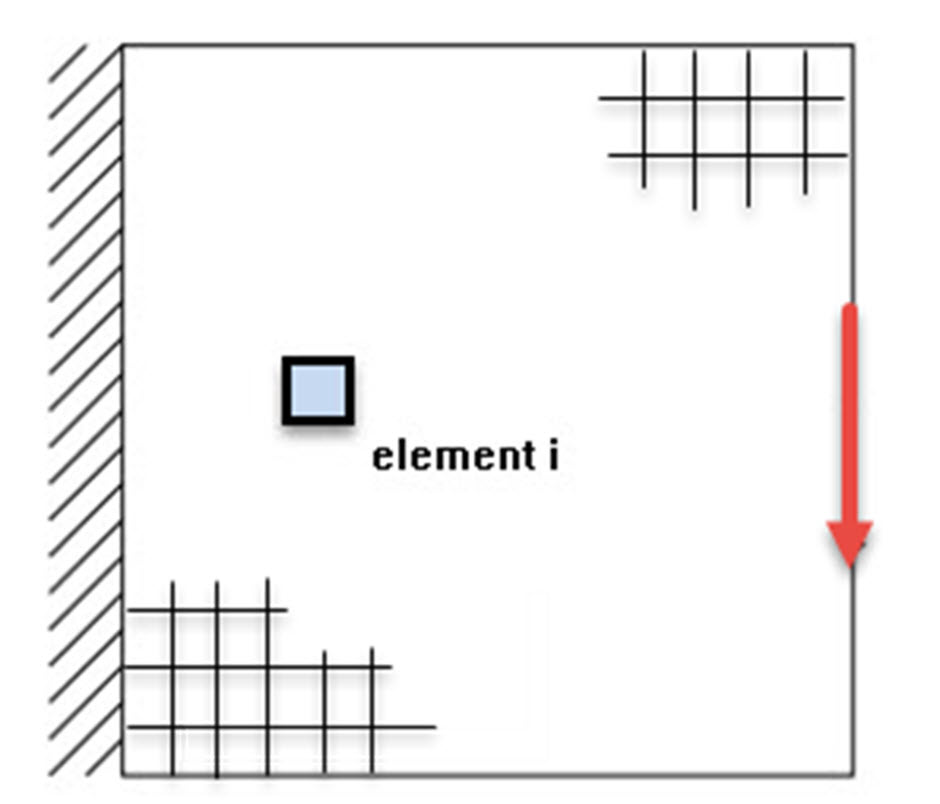
Figure 2 shows schematically the general concept. Element(i) is a typical element within the design space.

Figure 2. A schematic of FEA topology optimization

An initial FEA of this component will give a distribution of internal stress and deflection. Topology optimization seeks to improve the efficiency of the configuration by removing material, based on these FEA responses. Intuitively, we could do the job manually by starting to remove material which had a very low stress level. This type of approach is called an Optimality Criteria method. It is based on a heuristic idea – something which looks like a good approach from an engineering point of view. A formal implementation is called Fully Stressed Design (FSD). It is easy to implement and computationally cheap. Unfortunately, FSD does not work so well with multiple load paths, as found in most typical structures. Attempting to set all regions of the structure to very high stresses is not a realistic goal. FSD is sometimes used in a mixed strategy in combination with more sophisticated optimization objectives, such as minimizing strain energy.

 

Minimizing the strain energy can also be described as minimizing the compliance. Compliance is defined as the distributed force times displacement summation. Anything that minimizes the displacement distribution will maximize stiffness. Minimizing strain energy, or maximizing stiffness, or minimizing compliance are very closely linked concepts. All these are a global targets or objectives in that they are applied to the overall structure.

So how do we remove material from the mesh? In an FEA analysis it is efficient to keep the mesh constant throughout a series of model configuration changes. The assembly of element stiffness matrices into a system stiffness matrix at each iteration is then just a scaling process on local element stiffness values. Elements aren’t deleted, but instead scaled down toward a small stiffness limit. The stiffness terms don’t quite go to 0.0, as this would give singularities.

Historically there have been two main approaches. The evolutionary methods (ESO and BESO) aim to provide a ‘hard element kill’ approach. This means element(i) is either present, with full stiffness, or effectively eliminated, with a very low stiffness. Alternatively, the penalty driven method (SIMP) is described as a ‘soft kill’ method, and allows a gradation of stiffness range between the full value and a very low value.  There are other methods available, but I am going to focus on the SIMP method in this article.

SIMP method

The full title of the SIMP method is ‘Solid Isotropic Microstructure with Penalization’. That is a bit of a mouthful, but we will attempt to break it down. The term ‘Microstructure’ is included in the title because early work looked at developing material systems which were porous; made up voids and material in various distributions. Using this approach anisotropic materials such as foams, lattices and composites could be defined. This work has evolved in many interesting directions, including microstructure forms for lattice-type structures in additive manufacturing.  However, if the requirement is to work with conventional materials, then ‘Solid Isotropic’ representation is required.

As mentioned, stiffnesses will be allowed to vary throughout the mesh, between initial value and close to 0.0. The design variables are defined per element, not as the stiffness, but as a normalized value for density. The stiffness is assumed to be directly scaled by the density value. The term ‘density’ is a little confusing because the design variables are normalized values of between 1.0 and 0.0. So where does the ‘Penalization’ term come from? If a structure could develop any value of density between 1.0 (black) and 0.0 (white), we would get very large areas of ‘gray’ material. Gray areas are not physically meaningful for a solid isotropic material. We need to cluster distributions of density towards 1.0 representing the parent material, or 0.0 representing a void. The approach taken in SIMP is to penalize any density which is in the gray region. Figure 3 shows the penalty function used. The density is adjusted from its nominal value with a bias towards the extremes of 0.0 or 1.0. The order of the penalty function, P is often provided as a user control. Setting P higher than 1 will give more realistic structures with less gray. Somewhere between 2 and 4 is typically used – but it is worth experimenting to see the effect.

Inherently there will always be a blurred region of density, and hence stiffness, in the SIMP method. The method does not focus on traditional boundary region features, which develop stress concentrations. The structural and hence stress representation is not exact at a boundary. Local stresses should be viewed as a ‘smeared’ and averaged general indication. Similarly, the actual geometric boundary is not exactly defined. In part 2 of this article I will look at these implications for stress as both a constraint, and as an objective function – a possible alternative to compliance.

Figure 3. The penalty applied to intermediate densities

Mesh dependency

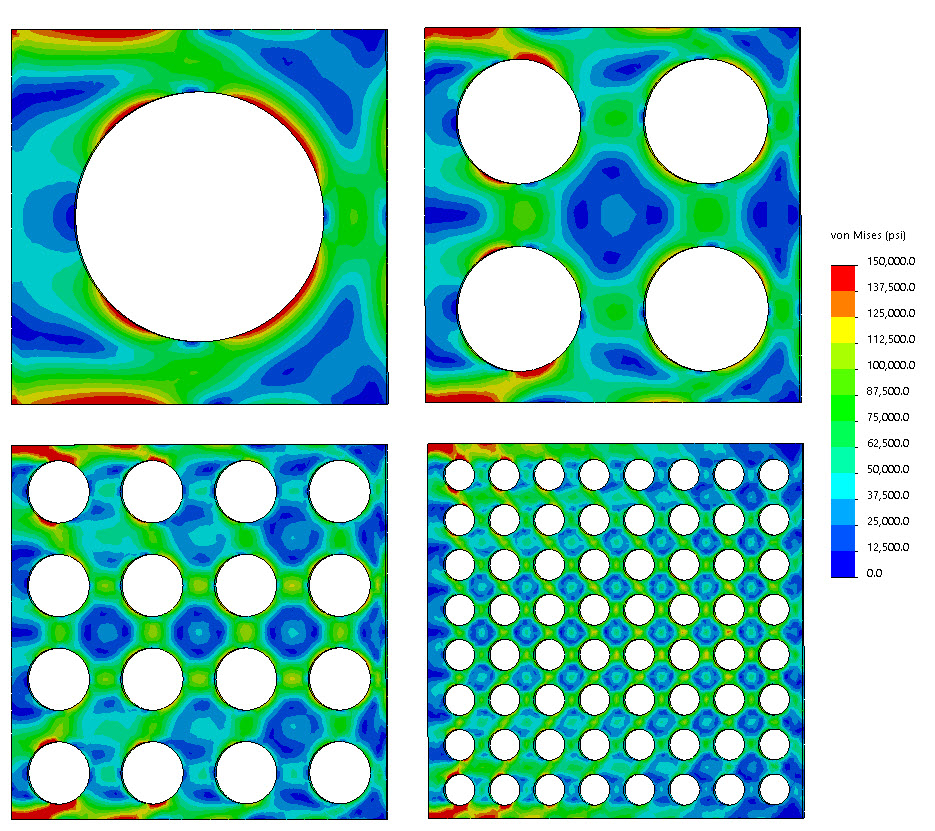
Figure 4 shows a series of models which have an increasing number of holes within them, running from one to 64. In each model the left-hand edge is fixed and the right-hand edge is loaded vertically, giving a shearing type response. The volume of material in each model remains the same at 65% of the volume without any holes. The resultant deflections are shown in figure 5.

Figure 4. Component with increasing number of holes and constant volume

 

Figure 5. Variation of perimeter deflection and compliance with number of holes

It is interesting to notice that as more holes are included, the right-hand edge deflection reduces. A plot of deflection against number of holes would show a clear tendency to converge to a finite deflection value. This shows that, in the limit, we can get the stiffest possible structure at 65% of the volume by having a distribution of very tiny holes. In fact, the solution is telling us that we should be really using a foam made of the parent material! If we are trying to design a structure using isotropic material then this is clearly a nonsensical result.  Figure 5 also shows that as the number of holes increases, the total perimeter is also increasing. We also see that the compliance is decreasing. The compliance is calculated as the applied force times the result resultant deflection. Compliance is one of the most popular measures of the efficiency of a structure in topology optimization.

Mesh dependency, with the tendency towards a high level of porosity, is one of the attributes of topology optimization that was discovered early on. For a specific optimization problem, given a target reduction in volume, the solution will depend on the element size within the mesh. A very fine mesh can drive towards a foam-like, ‘filigree’ or ‘fibrous’ configuration. The last two typically have many very thin strands of material.  A coarse mesh will constrain the optimization to a chunkier type of material distribution. It is clearly unreasonable to allow the density of the mesh to control the configuration an optimizer will deliver.

Various remedies were developed very early on to reduce this effect. There are three fundamental approaches.

• Perimeter control
• Density gradient control
• Density sensitivity filters

Perimeter control.

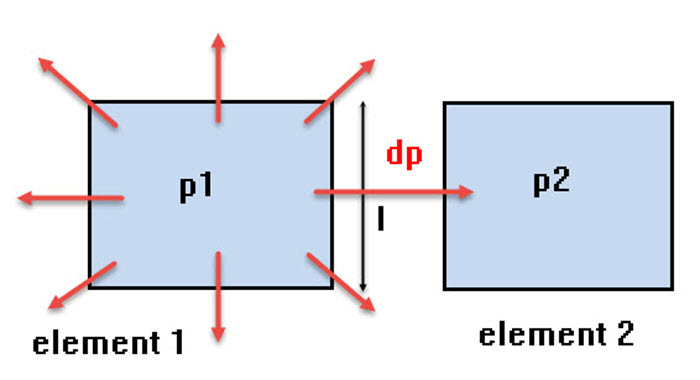
As we can see in figures 4 and 5, putting a limit on the perimeter to a value of 8.0, would limit the number of holes in our simple configuration to around 16. There are probably many different configurations of arbitrary shaped holes that could meet this target. But the target would clearly enforce a trend away from many small holes. One of the attractions of this method is that it is cheap to calculate and enforce this constraint in the optimization process. The main problem is that it is not physically meaningful as a parameter and is difficult to assign any kind of intuitive value to. A mathematical analogy is normally used which assesses the variation in density from each element to its set of neighbors. Figure 6 shows a simple schematic of this. Element 1 is being assessed by measuring the density jump, dp = p2-p1, to one of its neighbors, element 2. This density jump is weighted by the element edge length L. The summation of all dp * L is made for element 1. The same process continues throughout the mesh and all values are summed. A constraint is applied to this total value, hence suppressing the tendency for density change across elements. This does have the advantage of being a global constraint, but again it is difficult to come up with a good value and quite a few experimental runs are needed to assess the influence.

 

Figure 6. Perimeter control methodology

 

Density gradient control.

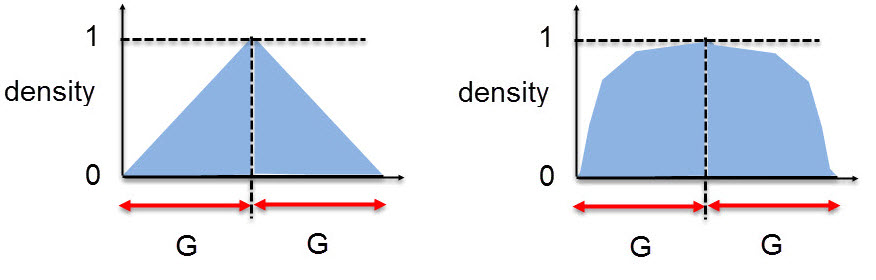
In this method, a physically meaningful length G, is defined as being a limit on the gradient of the density. The length G spans an arbitrary number of elements. Figure 7(a) shows the idea schematically. Because the maximum density is 1.0 and the minimum is 0.0, then the steepest gradient is shown acting over length G. This means we are forcing the material distribution to clump together over the distance 2G, as shown. Hence this gives an effective minimum member size. In practice because the penalty is applied to intermediate densities during iteration steps, the distribution will migrate to that shown in figure 7(b).

Figure 7 (a) left. Density gradient control before penalty application. (b) right. After application

In practice, more sophisticated variations are used within the optimizers, as it would be expensive to apply the huge number of constraint equations that this implies. However, the basic principle remains.

Density sensitivity filters

These methods use the sensitivity of the optimization responses. As the density of an element is changed, then the global compliance will change slightly. This is the sensitivity that is being used. Each element in the mesh in turn becomes a target. A fixed distance r is defined around each target element, as shown in figure 8. From the target to the perimeter of the circle with radius r, all surrounding element sensitivities are forced to follow a linear decrease to a value of 0.0 at the perimeter. The effect of this is to eliminate any voids within the area or volume defined by r and to enforce a ‘gray’ type of distribution of decreasing density. However, because the overall optimization task is iterative, the penalty distribution method will rapidly migrate this distribution towards a sharper distinction between material and nonmaterial (density 1.0 and density 0.0 respectively). It will thus suppress fibrous or filigree type configurations with width less than 2r.

Figure 8. Density sensitivity filter method

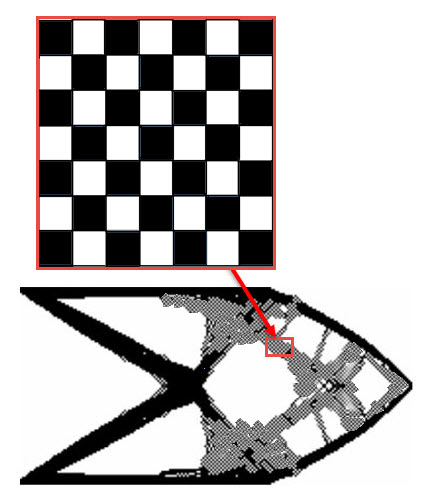
Checkerboarding

There is a tendency for elements to mesh together into a pattern which is similar to a checkerboard, as shown in figure 9. Alternating elements are connected only at the corner nodes, leaving voids between. For many types of elements this is a stable configuration which does not cause any problems with the FEA solution. It is of course a physically meaningless solution, but as in the case of the foam-like solutions seen earlier, it is numerically a relatively stiff solution. It is in fact stiffer than any equivalent ‘sensible’ material distribution. So, it will minimize compliance and be very attractive as a solution to the Optimizer!

 

Figure 9. Typical checkerboarding result

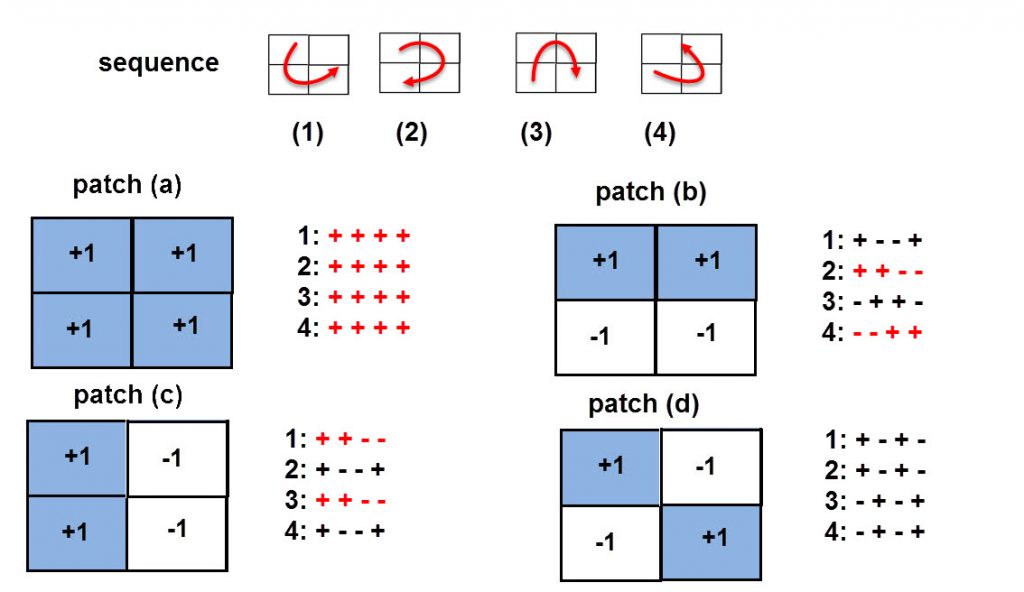
Various ways have been developed to suppress this effect. The mesh dependency control methods described earlier will tend to minimize the checkerboarding effect. However, relying only on these controls would mean that thin member solutions would always be suppressed, unless the controlling distance was set very close to the element size. More specific, checkerboarding, controls look directly at the connectivity logic in a group or patch of elements. This is shown schematically in figure 10.

Figure 10. Connectivity logic assessment in checkerboarding

A patch of four elements can have one of four configurations as shown by patch (a) through patch (d) in Figure 10. A set of four sequences (1) through (4), moving between these elements are shown in the upper sketch. A pattern describes how the elements flip between non-zero density, (+1) and zero density (-1).  The various patterns are shown to the right of the patch configurations. A monotonic sequence (colored red) is defined as one which stays constant, increases or decreases. An oscillating sequence (colored black) flips between positive and negative. All patches except patch (d) show at least one example of a monotonic pattern. So, each patch of elements within the mesh is searched for at least one monotonic sequence. If none are found, then there is a checkerboard patch present and this can be eliminated by smearing effective material over all four elements in the patch.

There are quite a few variations on this technique.

Conclusion

 

The basic numerical approach behind the SIMP method has been shown, together with provisions for mesh independency and checkerboarding. In part 2 we will look at the alternative objectives and constraints available.  We will also see how manufacturing constraints are enforced, and derive some general guidelines for controlling topology optimization.

 

[1] https://grabcad.com/challenges/ge-jet-engine-bracket-challenge

[2] https://sffsymposium.engr.utexas.edu/sites/default/files/2014-110-Carter.pdf