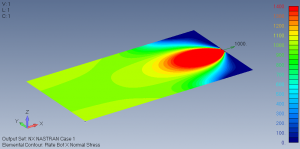
Video : 60 minutes presentation and curated Q and A Over-constrained, under-constrained or somewhere in the middle with FEA! Boundary conditions are probably the most difficult aspect of static FEA Underconstrained models: It is easy to forget to apply adequate constraints – Rigid Body Modes result! Over constraining is more subtle: The physics of the […]
Gimme a ticket for an aer-o-plane
Have you heard the 1967 hit from the Box Tops, released later by Joe Cocker? Gimme a ticket for an aer-o-plane Ain’t got time to take a fast train Lonely days are gone, I’m a-goin’ home ….. Ok, that dates me – but check it out, it’s a great song. I should have subtitled this […]
Session 2: FEA quick sanity checks
Session 2: FEA quick sanity checks 30 minutes presentation, 30 minutes curated Q and A Making sure we don’t fall into the trap: “Garbage in – Garbage out” is vital in FEA. I show some sanity checks we can use in static and dynamic analysis to quickly make sure we are on the right […]
Session 1: St Venant’s Principle
Session 1: St Venant’s Principle 30 minutes presentation, 30 minutes curated Q and A This principle is often quoted in FEA. It is a very generalized statement, but what does it mean and how can we use it in practice? I explore the background to the principle and discuss how it can be used […]
Session 3: Free Body Diagrams
Session 3: Free Body Diagrams – what are they and why do they go wrong? 30 minutes presentation, 30 minutes curated Q and A Free body diagrams are used in structural analysis to try to reduce the problem to its simplest description. Where does the load get applied and where does the load get […]
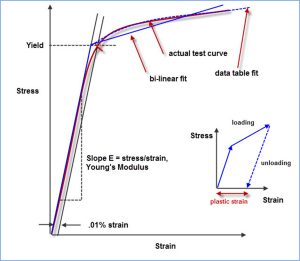
Who’s on First; Hooke or Young?
A Good Question I was teaching the “Introduction to Finite Element Analysis” training course in Holland recently. A design engineer on the course came up with a good question relating to a graph I had just sketched up on the whiteboard. I was describing how a material will respond to the loading, in terms […]