I have been providing e-learning courses on FEA for over 11 years. I now supplement the courses with a free weekly broadcast that covers topics across FEA. Format – live presentation around 30 minutes. Q and A 30 minutes . Completed presentation recordings to view Session 1. St Venant’s Principle […]
Session 6: High Cycle or Low Cycle fatigue – what’s in a number?
What’s the real story behind the transition from Low Cycle to High Cycle fatigue? Video : 60 minutes presentation and Q and A The terms High Cycle and Low cycle fatigue are used extensively – but what is the real difference? Is the transition an arbitrary number; 1000 cycles, 100,000 cycles. As […]
Session 11: Units in FEA – some horror stories!
Units can cause a lot of errors in FE Analysis… Video : 60 minutes presentation and curated Q and A Conversion between unit systems is one of the biggest problems The errors can be due to simple ‘finger trouble’ Or They can be very difficult physical units US (old Imperial) to Metric is probably the most […]
Session 13: FEA models under or over constrained!
Video : 60 minutes presentation and curated Q and A Over-constrained, under-constrained or somewhere in the middle with FEA! Boundary conditions are probably the most difficult aspect of static FEA Underconstrained models: It is easy to forget to apply adequate constraints – Rigid Body Modes result! Over constraining is more subtle: The physics of the […]
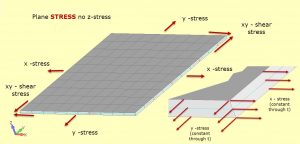
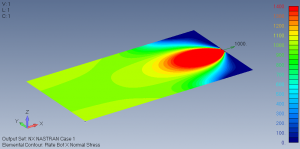
Plane Stress and Plane Strain – simplifying models
Background A previous article explained that even with powerful modern computers, there is often a motivation to use simplifying techniques in Structural FE Analysis. This follow-on article describes how two closely related methods can be used to take 2D slices through a complex structure at regions of interest. The resulting FEA models can give valuable […]
Session 1: St Venant’s Principle
Session 1: St Venant’s Principle 30 minutes presentation, 30 minutes curated Q and A This principle is often quoted in FEA. It is a very generalized statement, but what does it mean and how can we use it in practice? I explore the background to the principle and discuss how it can be used […]